【問題】
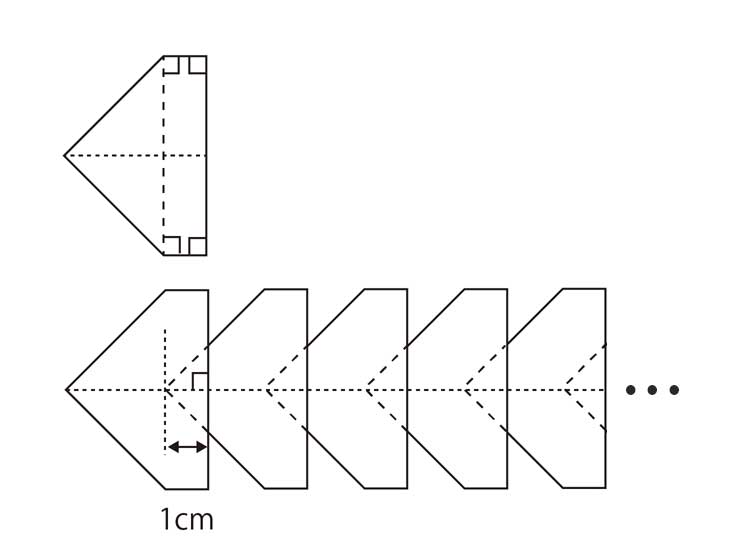
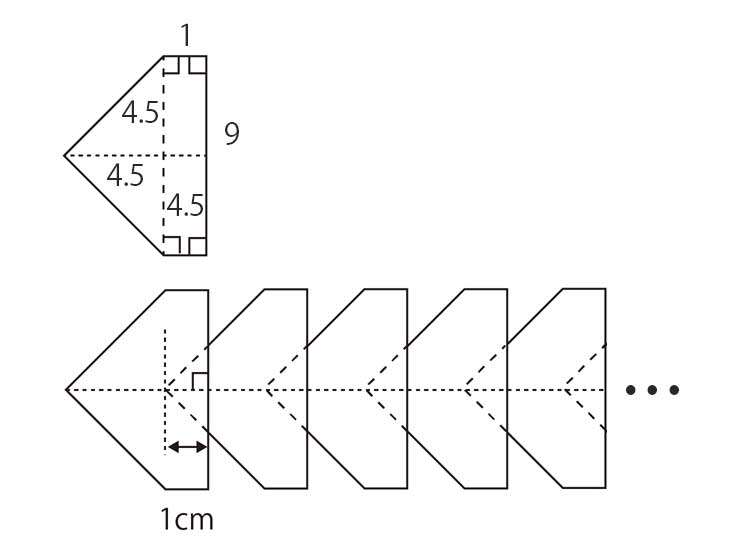
一辺が4.5㎝の直角二等辺三角形2つと、たて9㎝、よこ1㎝の長方形を組み合わせた五角形がある。この五角形を2つの二等辺三角形が重なるように折り目を付ける。この折り目が1㎝重なるようにのりではり、同じ五角形を100個ならべていく。この時、並べて出来た図形の面積を求めなさい。また、求め方を式と言葉で説明しなさい。
- ヒント
-
まずは問題に数字を書き込む
図形問題で重要なことはまず、数を書き込むことです。これをしないと、頭を余計に使ってしまいミスが発生しやすくなります。
考え方(その1)
この問題は同じ図形が100個並んでいて、重なっている三角形が99個だから99個引けばいいと考えるのはお勧めしません。理由は重なるということを考えた時に、立体で考える必要が出てくるので頭を余計に使ってしまいます。そこで、その2の方法がおすすめです。
考え方(その2)
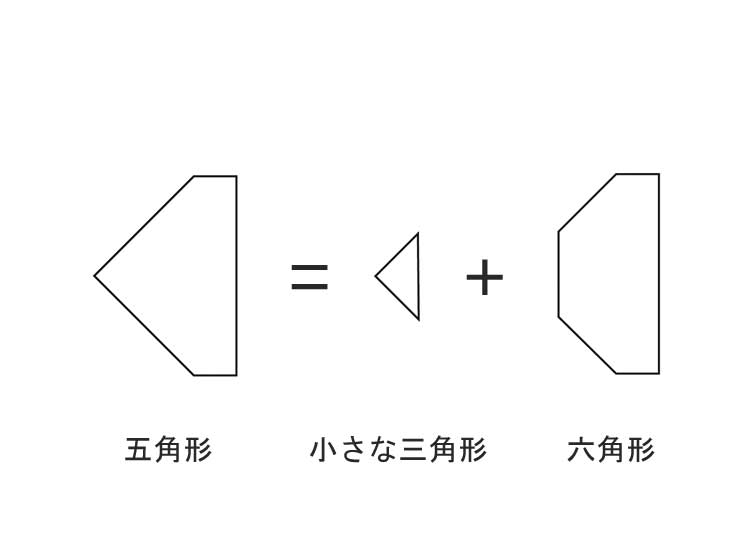
これは一番左の図形は小さい三角形(重なり部分と同じ面積)とそれを取り除いた六角形の図形と考えて、小さい三角形1つと六角形100個で考える解き方です。この考えであれば、「重なり」を考える必要がないため平面で考えることが出来ます。平面であれば立体より頭を使わないため、おすすめの解き方になります。
- 答え
-
【面積： 2826㎠】
【求め方】
まずは大元の五角形の面積と重なり部分の小さな三角形の面積を求めます。
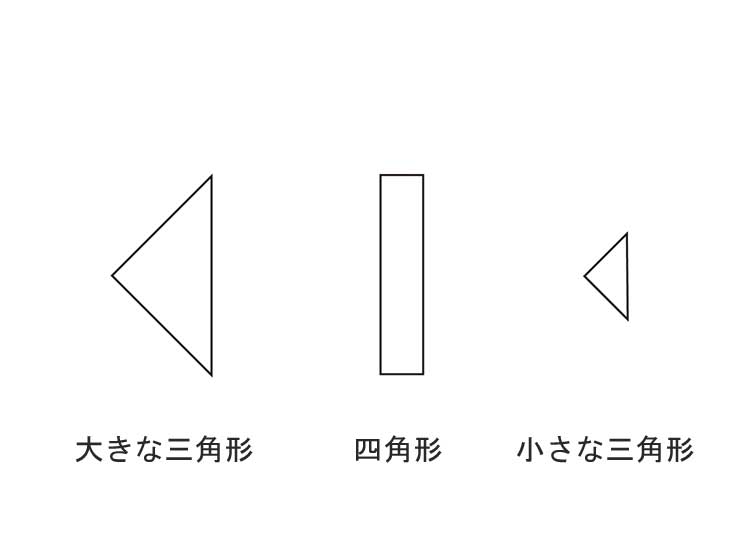
図形を「大きな三角形」「四角形」「小さな三角形」に分けて考えていきます。
◆大きな三角形の面積
二等辺三角形が二つなので面積を出したら個数をかけます。
4.5×4.5÷2×2=20.25㎠
◆四角形の面積
9×1=9㎠
◆小さな三角形(重なり部分)の面積(重なり部分)
1×2÷2=1㎠
よって、五角形の面積は29.25㎠
次は、一番左の五角形を小さい三角形と六角形に分けます。小さな三角形(重なり部分)の面積は
1㎠
五角形の面積は29.25㎝なので、六角形の面積は
29.25-1=28.25㎠
小さな三角形が1つと六角形が100個になるので
1+28.25×100＝2826㎠
となります。
どんな解き方がいいのか
出来るだけ頭を使わない解き方を心がけることが重要です。脳がキャパオバーになることを防ぐことで、受験本番でミスが発生しにくくなります。
